Quelle est la formule de l’énergie électrique ?


A lire aussi : Comment estimer avec précision la valeur de votre maison ?
Plan de l'article
Énergie éolienne instantanée
Une éolienne est une machine qui, par définition, convertit l’énergie éolienne en énergie mécanique. Tout d’abord, il est nécessaire de quantifier la source d’énergie disponible, c’est-à-dire l’énergie associée au vent. Si le vent a une certaine vitesse « V » à un moment donné et traverse une certaine surface « A », la force instantanée du vent est due à la relation suivante :
Pvent = 1/2 Rho* A*V3
A lire en complément : Quel est le fruit qui pousse le plus vite ?
où « Rho » est la densité de l’air, qui est d’environ 1,2 kg/m3 à 20 °C, au niveau de la mer.
Néanmoins, cette relation met clairement l’accent sur :
- que la puissance éolienne disponible à un certain moment dépend du cube de vitesse du vent. Enfin, si vous avez un vent 2x plus rapide, vous aurez 8x plus de puissance. Nous comprendre la valeur de placer des éoliennes dans des endroits venteux. Par conséquent, ce n’est pas un caprice d’un technicien puriste, nous voyons que le potentiel énergétique dépend fortement de la vitesse du vent. C’est une condition nécessaire, pas une option.
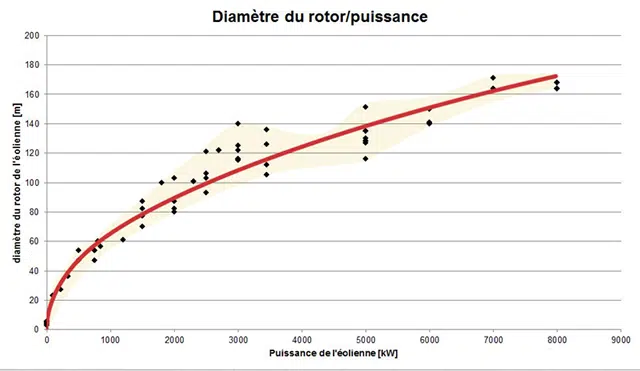
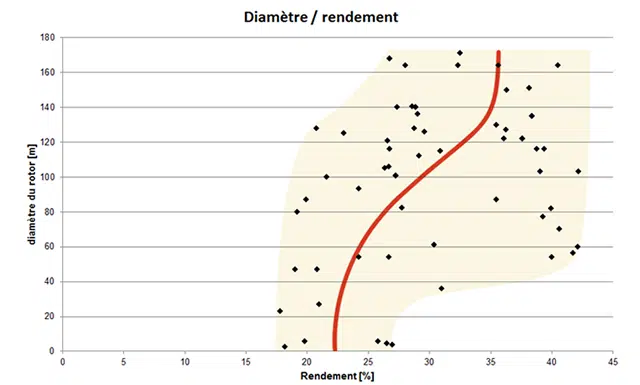
- que la puissance disponible dépend directement de la surface traversée par le vent. Si elle est considérée comme équivalente à la surface dessinée par le rotor d’une éolienne, la puissance éolienne instantanée (évaluée par la relation ci-dessus) représente la puissance maximale disponible que l’éolienne peut convertir. On sait que la surface balayée par une éolienne dépend du rayon de son rotor (π* r²). En conséquence, la puissance disponible dépend du carré du rayon de l’éolienne. En résumé, si vous avez un rotor 2 x plus long, vous aurez 4 fois plus de puissance.
Schéma montrant le rapport entre le diamètre du rotor et la puissance maximale des éoliennes : Fabriqué à partir de fiches techniques de 62 modèles d’éoliennes plus récents
.
- que la densité de l’air a un impact sur la puissance disponible. On sait que la densité de l’air dépend de la température, de l’humidité et de la pression atmosphérique. Selon ces paramètres, vous pouvez obtenir des fluctuations de 20% de densité, et donc la force actuelle du vent. Ainsi, au niveau de la mer par – 10 °C, un mètre cube d’air pèsera 1 341 kg, alors qu’à 30° C il ne pèse que 1 164 kg d’air.
L’ énergie du vent
Connaître la puissance instantanée du vent est une chose, mais ce qui nous intéresse, c’est son énergie. Il y a donc une idée du temps qui doit intervenir quelque part. Afin de connaître l’énergie du vent sur une certaine période de temps, il est nécessaire d’utiliser sa puissance dans le même Période. La connaissance de la vitesse moyenne du vent ne suffit pas, il est nécessaire de changer la vitesse pendant la période d’enquête et de résumer les contributions.
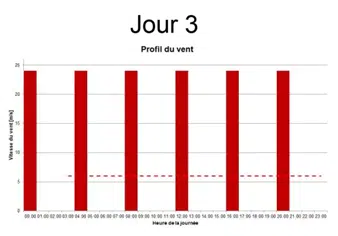
Prenons une période de 24 heures et comparons trois jours venteux avec un vent moyen de 6 m/s pour chacun, mais un profil de distribution différent :
****
Si les vitesses moyennes sont les mêmes, alors le profil de distribution est très différent entre ces trois jours. Un simple calcul permet de constater que la quantité d’énergie fournie par le vent sur 24 heures par m² pour chaque profil est radicalement différente.
- Jour 1:24 x 6³ x 1 x 1,2 = 6220 Wh = 6,22 kWh
- Jour 2:12 x 12³ x 1 x 1,2 = 24 880 Wh = 24,88 kWh
- Jour 3:6 x 24³ x 1 x 1,2 = 99,530 Wh = 99,53 kWh !
Donc, nous voyons clairement que nous ne pouvons pas la moyenne de la vitesse du vent et de la répartition du vent sont cruciales pour calculer l’énergie éolienne sur une certaine période et sur une certaine superficie.
Nb : Lorsque les éoliennes actuelles atteignent leur puissance maximale d’environ 10-15 m/s, les vents plus forts ne sont pas pleinement utilisés : l’éolienne est freinée pour maintenir son intégrité.
Explication avec une formule
Supposons que les mesures du vent soient disponibles à intervalles réguliers pour une période de plus ou moins par année. L’intervalle entre chaque mesure est de « dt » secondes et le nombre d’échantillons est mesuré « N ». Par conséquent, la durée de la période d’observation, « T », est n*dt. Nous obtenons un échantillon de différentes vitesses, U1 à ONE. Il est donc possible d’estimer facilement la vitesse moyenne du vent pendant cette période de mesure :
Um = (1/N) * (U1 U2 … UN-1 UN)
Pour produire de l’énergie, il est nécessaire de résumer les contributions des différentes mesures. Si la force du vent associée à une mesure de la vitesse de l’interface utilisateur
Pi = 1/2* Rho* A* (Ui) 3
L’ énergie éolienne, Ev, vaut alors : Ev = (P1 P2 … PN-1 PN) *dt. En fait, il est nécessaire de connaître l’évolution de la vitesse du vent tout au long de la période d’enquête. Si on connaissait la vitesse moyenne du vent, ça ne suffirait pas à déterminer l’énergie, Ev. En fait, l’énergie éolienne ne peut pas être calculée à partir de la vitesse moyenne (comme suit) :
Ev n’est pas égal à 1/2*Rho*A* (Um) 3*T
Cette différence est chiffrée dans la section suivante et est loin d’être négligeable.
Distribution du vent : statistiques d’approche
Dans la section précédente, nous avons intégré les différents pouvoirs pour obtenir de l’énergie éolienne pendant la période visée par l’enquête. Il existe une autre approche, qui a également l’avantage de synthétiser les propriétés du vent dans la période à l’étude. C’est la fonction de distribution du vent, qui est appelée p (V) ici.
Imaginons que nous sommes intéressés par les vitesses du vent. Ceux-ci varient entre la valeur zéro et la vitesse maximale appliquée. Cet intervalle est coupé en plusieurs petites plages de vitesses de largeur DV. Le produit p (V) *dV indique que la vitesse du vent pendant la période d’observation est une valeur de V (appelée « T »). Cette valeur varie entre « 0 » et « 1″. La valeur est zéro si le vent n’atteint jamais cette vitesse, et la valeur est 1 si le vent est toujours à la vitesse V, qui est dans la La pratique n’arrive jamais. Par exemple, si la probabilité p (V) *dV que la vitesse est égale à V est de 0,5, cela signifie simplement que la vitesse V atteint la moitié du temps d’observation. Cela peut sembler assez abstrait, mais il est difficile d’ignorer ce concept si nous voulons introduire des approches statistiques pour l’évaluation de l’énergie éolienne.
Une fois cette fonction connue, la contribution de la vitesse V à l’énergie éolienne peut être déterminée comme suit :
Ev (V) = 1/2*Rho*A*V3* (p (V) *DV*T)
Nous obtenons ensuite l’énergie du vent en additionnant les différentes gammes de vitesses. En d’autres termes, chaque plage de vitesses est présentée à une certaine fréquence pendant la période d’étude, « T », et correspond à une certaine contribution à l’énergie totale. Afin d’obtenir de l’énergie éolienne, toutes les gammes de vitesses rencontrées et leur contribution sont prises en compte.
Comment obtenons-nous cette fonction de distribution ? La méthode la plus cohérente consiste à utiliser les valeurs de vitesse mesurées et à étudier la fréquence des vitesses différentes. C’est la situation idéale.
Toutefois, ces mesures peuvent ne pas être disponibles ou au moins des mesures lacunaires qui ne définissent pas correctement la fonction de distribution. Par exemple, le potentiel éolien peut varier d’une année à l’autre, de sorte qu’il faut plusieurs années de mesure pour établir un comportement moyen. La littérature prend souvent des années de mesure de 10 ans. Il est donc évident qu’il n’est pas toujours possible d’évaluer le potentiel sur une période aussi longue. Dans ce cas, on peut supposer comment les vitesses sont dans le temps rencontré. Dans l’énergie éolienne, la fonction la plus courante de la fonction de distribution de Weibull est.
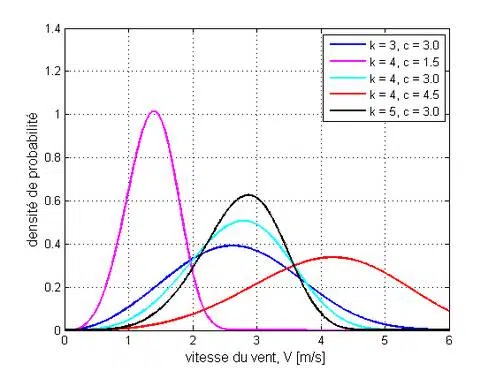
Exemples de distributions de Weibull pour différents ensembles de paramètres.
La fonction Weibull est illustrée dans le graphique ci-dessus. Il n’a que deux paramètres : le facteur de forme k et le facteur d’échelle c. Cela signifie que nous ne savons à quelle fréquence les différentes vitesses du vent, V, sont rencontrées pendant la période d’observation, si la valeur de deux coefficients peut être réglée. Le but du jeu est de fixer ces deux coefficients en fonction des données lacunaires disponibles. En d’autres termes, on ne peut reconstruire l’histoire de l’intérêt du vent que si l’on peut utiliser les deux paramètres du Weibull : principalement basés sur la vitesse moyenne du vent et la variance. La qualité de cette méthode est correcte si la distribution du vent à l’endroit étudié suit réellement une distribution de Weibull. Ce sera une question du spécialiste. Le lecteur est invité à se référer à un travail plus approfondi, si ce sujet l’intéresse. Notez que nous entendons également parler de la fonction de distribution de Rayleigh, qui est plus simple en ce qu’elle n’a qu’un seul paramètre (c’est un cas particulier de la fonction Weibull).
Par exemple, commentons la figure ci-dessus, qui montre 5 ensembles différents de paramètres pour la fonction de distribution de Weibull. Par exemple, nous voyons la courbe « rouge », qui représente les vents à une vitesse moyenne proche de 4,25 et qui oscille largement autour de cette valeur. La courbe « noire » représente les vents à vitesse moyenne inférieure (près de 3,5) et présente une variation significativement plus faible (près de 3m/s) et présente une variation beaucoup plus faible autour de cette moyenne.
En résumé, les fonctions de distribution du vent peuvent avoir deux utilisations. D’une part, ils permettent de synthétiser les propriétés intéressantes du vent en termes de production d’énergie, et d’autre part, en utilisant des fonctions prédéfinies telles que la fonction Weibull, ils permettent d’utiliser l’évaluation de l’énergie éolienne, ne serait-il que des données lacunaires sur son développement à un certain niveau de localisation sont disponibles. Dans ce dernier cas, nous devons être conscients que la qualité de cette méthode est inférieure à une campagne de mesure sur une décennie. Dans le meilleur des cas, les résultats auront la même valeur.
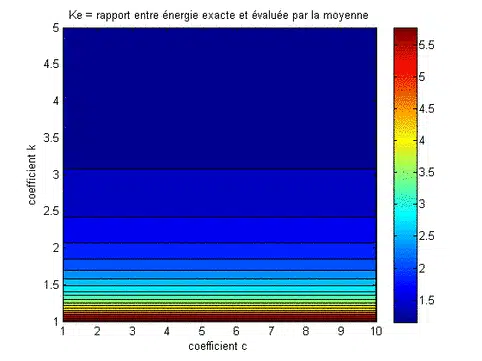
|
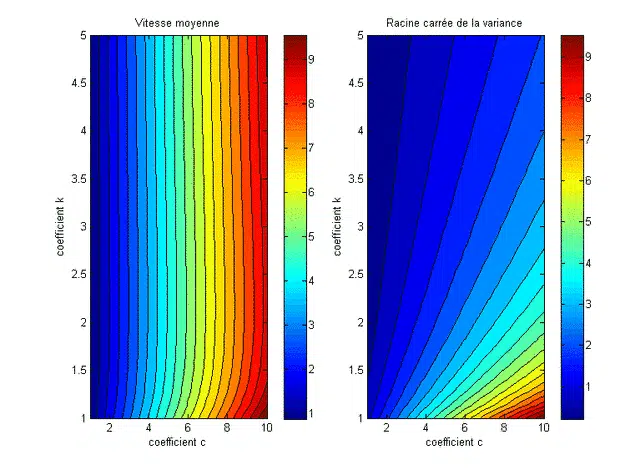
Pourquoi ne pas évaluer directement l’énergie en fonction de la vitesse moyenne ? Ce n’est pas pareil ! La force instantanée du vent est obtenue en prenant le cube de vitesse. L’énergie est alimentée par le Période de mesure obtenue grâce à l’intégration de ces services. Mathématiquement, il est différent d’intégrer la vitesse au fil du temps, puis de la rouler. En d’autres termes, l’ordre dans lequel vous effectuez les opérations d’intégration et Power 3 est important : nous définissons d’abord la vitesse actuelle sur le cube, puis résumons les diverses contributions au cours de la période analysée. Est-ce une grosse erreur si nous évaluons l’énergie éolienne en vitesse moyenne ? ouais ! En raison des cas survenus, il est facile de sous-estimer 100% ou plus. Vous pouvez essayer de voir ce qu’il y a avec la fonction de distribution Weibull. Avant, en entrant dans le focus du sujet, on peut d’abord se faire une idée du développement de la vitesse moyenne et de la variance, en fonction du développement des deux paramètres de la fonction Weibull, le paramètre de forme, k et paramètre d’échelle c On peut voir que la vitesse moyenne du vent dépend principalement du facteur d’échelle, c. La variance, quant à elle, dépend fortement des deux facteurs. Enfin, nous présentons maintenant le rapport d’énergie éolienne calculé à l’aide de la fonction de Weibull et de l’énergie éolienne, qui est calculé approximativement par la moyenne de la fonction Weibull. Ce rapport est connu sous le nom de Factor Ke Ke = Somme (1/2*Rho*a*Ui³/n)/(1/2*rho*a*um³) = (1/N somme (Ui³))/(um³) ****** 8 Conclusion : Le rapport Ke peut être très important, plus que le facteur de forme k est faible. Il a été constaté que cela dépend uniquement de la valeur de ce facteur k. ci-dessous est un tableau des nombres :
|
Courbe de performance et efficacité instantanée
Ainsi, le vent a de l’énergie pendant une certaine période de temps. Cette énergie est convertie par l’éolienne en énergie mécanique et certainement en énergie électrique. Cette transformation peut être divisée en plusieurs étapes :
- L’ énergie cinétique du vent est convertie en travail moteur sur l’axe du rotor. Cette transformation est réalisée avec un certain rendement, aérodynamique.
- Le travail du moteur sur le rotor est transféré à l’axe du générateur avec un certain degré d’efficacité et d’efficacité mécanique de l’embrayage.
- Le générateur convertit le travail du moteur sur son axe en énergie électrique avec une certaine quantité de efficacité électrique.
Le revenu total est le produit du revenu de ces trois niveaux. Il est difficile d’évaluer ces trois rendements de façon simple et, par conséquent, d’estimer le rendement global. Le moyen le plus simple est de mesurer ce qui vient de l’éolienne pour avoir une idée de l’efficacité globale.
Le rendement global d’une éolienne, V, est défini comme le rapport entre la puissance électrique indiquée par le générateur et le Pvent :
eta (V) = efficacité instantanée à la vitesse V = Pelec (V) /Pvent (V),
L’ énergie éolienne immédiate a été réglée en haut de cette page. Il reste connu sur la puissance électrique chargée par l’éolienne en fonction de la vitesse V, alors qu’il est connu que les détails des pertes successives ne peut être expliqué à n’importe quel stade de la transformation. De plus, si l’alimentation électrique coupée en fonction de la vitesse du vent peut être connue, la puissance électrique annuelle de l’éolienne peut être évaluée à l’aide de mesures du vent in situ :
Aelec = (Pelec (V) 1 Pelec (V) 2 … Pelec (V) N) *dt.
La courbe de puissance caractéristique d’une éolienne fournit la puissance électrique en fonction de la vitesse du vent. En général, ces courbes sont signalées par les fabricants d’éoliennes. Pour les grandes éoliennes, la courbe caractéristique a été certifiée par un laboratoire et dans des conditions d’essai standard. Il y a donc une certaine certitude quant aux performances réelles de l’éolienne. La situation est plus critique pour les petites éoliennes produites par des fabricants relativement petits. En fait, ils fournissent généralement le courbe de performance caractéristique de leur appareil, mais certifient rarement les performances. Par conséquent, il y a peu ou pas d’assurance quant à la fiabilité du rendement annoncé. Dans tous les cas, la certification des performances est un élément à prendre en considération lors de l’achat d’une éolienne, surtout lorsqu’il s’agit de concepts innovants ou « potentiellement » révolutionnaires (si non-fumeur).
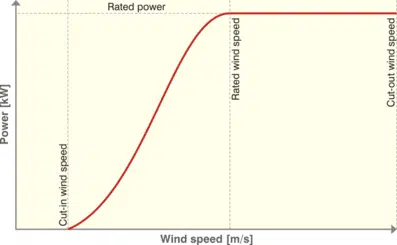
La courbe de puissance caractéristique se compose de trois paramètres principaux (voir figure ci-dessous) :
- Vitesse minimale d’amorçage : Il s’agit de la vitesse du vent à laquelle l’éolienne commence à charger de l’énergie utile (c’est-à-dire l’énergie électrique).
- Vitesse maximale du vent de coupure : Il s’agit de la vitesse maximale acceptable pour l’éolienne. En outre, la résistance mécanique de ces différents composants n’est plus garantie (ou simplement planifié). Lorsque la vitesse du vent est plus élevée, l’éolienne est idéalement coupée automatiquement pour maintenir son intégrité.
- Puissance nominale : Cette valeur correspond souvent à la puissance électrique maximale qui peut être obtenue à partir de l’éolienne. Cela ne se produit jamais à la vitesse maximale acceptable du vent. En fait, juste avant que la vitesse d’arrêt soit atteinte, des dispositifs sont utilisés pour freiner la vitesse du rotor (dynamique ou aérodynamique), ce qui peut affecter de manière significative les performances du rotor. l’éolienne.
En résumé, nous trouvons généralement des courbes de performance avec l’apparence suivante.
Forme typique de la courbe de performance d’une éolienne : production finale d’aliments électriques en kW en fonction de la vitesse actuelle du vent en m/s.
La puissance nominale d’une éolienne ne signifie rien sur son efficacité, si le fabricant ne mentionne pas comment la vitesse du vent recevra cette énergie électrique. En fait, il n’est pas possible de déterminer la force instantanée du vent, et donc de déterminer son efficacité globale instantanée.
|
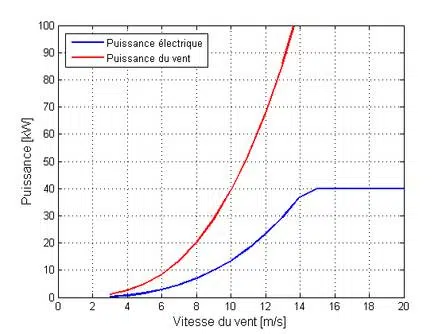
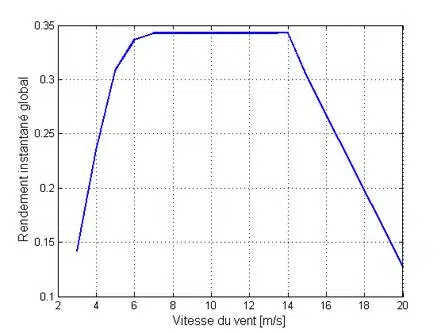
Exemple : FairWind F64-40 Par exemple, la société wallonne ****10 FairWind, fondée à Seneffe, vend des éoliennes à essieu vertical dont les courbes de performance sont disponibles sur son site web. Lors de l’analyse de votre modèle F64-40, les courbes résultantes sont affichées ici : Performance du système de détection de couteaux à axe vertical Fairwind F64-40 tel que spécifié par le fabricant. La vitesse minimale de 3 m/s, la vitesse maximale de 20 m/s et la puissance nominale de 40 kW obtenue à 15 m/s sont clairement distinguées.
|
Estimation de la production d’électricité
Sur la base des mesures
Sur la base de la mesure du vent réalisée sur une période T et de la courbe de puissance caractéristique de l’éolienne, la production électrique de l’éolienne pendant cette période peut être évaluée sera :
Aelec = (Pelec (V) 1 Pelec (V) 2 Pelec (V) 3 … Pelec (V) N) *dt
Lorsque nous effectuons une mesure de vitesse toutes les secondes « dt », nous avons des valeurs « N » dans notre échantillon telles que T = N* dt. En bref, on suppose que la vitesse mesurée en un point, Vi, reste constante tout au long de l’intervalle de mesure, dt. Pendant un intervalle L’éolienne produit Pelec (V) i*dt. Nous faisons enfin la somme à tous les points de mesure pour obtenir l’énergie électrique finale.
Sur la base de la répartition statistique
Une autre option consiste à travailler sur la base de la distribution statistique, dont les paramètres sont connus (basés sur des mesures ou des simulations) :
Eelec (V) = Pelec (V) * (p (V) *DV*T),
où dans le membre droit le premier facteur est la puissance électrique produite à la vitesse V, et le second facteur est le temps total pendant lequel la vitesse est égale à V (pendant la période de mesure T). L’énergie finale, Eelec, est obtenue en résumant toutes les vitesses rencontrées.
Certains fabricants utilisent cette méthode pour estimer la production annuelle d’électricité de leurs éoliennes. En fait, ils définissent les paramètres de la fonction de distribution p (V) et regardent ce qui en résulte au niveau de la production. Si vous entendez des estimations de la production électrique, vous devez savoir que le fabricant a fait des hypothèses sur la façon dont les vitesses se produisent au fil du temps. En général, le vent sur votre site n’est pas le même que le vent qu’il a pris en compte dans son estimation. Pour être strict, vous devez s’assurer que le fabricant communique ces paramètres. C’est la seule façon de comparer différents matériaux les uns avec les autres sur la base d’estimations de la production électrique.
Rendement total estimatif des éoliennes
Il est également possible de connaître la puissance moyenne de l’éolienne pendant la période d’observation, T. D’une part, l’énergie éolienne disponible (source d’énergie), l’événement et, d’autre part, l’énergie électrique produite par l’éolienne Eelec (telle que calculée ci-dessus). Le rapport de ces deux valeurs donne le rendement moyen :
Rendement total moyen = Eelec/Événement,
Par global, nous voulons dire que nous sommes intéressés par ce qui arrive et sort de l’éolienne dans le monde entier. En règle générale, un rendement moyen de 20% pour les petites éoliennes et 35% pour les grands modèles.
Nombre de Heures d’ouverture
La puissance chargée par une éolienne dépend de la vitesse du vent. Par conséquent, le plus souvent, l’éolienne ne fonctionne pas à puissance nominale (PN), puisque le vent n’est généralement pas suffisant pour assurer cela. C’est l’un des arguments des critiques des éoliennes. Comparativement aux centrales conventionnelles à base de fossiles (typiquement une centrale TGV) ou aux centrales nucléaires qui fonctionnent continuellement près de leur capacité nominale, une éolienne fonctionnera principalement à une capacité inférieure à PN. Par conséquent, les éoliennes auront besoin d’une capacité installée plus élevée que les centrales conventionnelles pour obtenir la même production annuelle d’énergie. Il s’agit d’un argument assez controversé, bien que techniquement très clair. L’objectif n’est pas de faire le point sur cette question. On reprend juste l’argument ici.
Une façon de commencer la production d’un L’éolienne doit rendre compte de son rendement annuel en nombre d’heures de fonctionnement à puissance nominale. En d’autres termes, nous calculons le nombre d’heures que l’éolienne nominale devra conduire pour charger la même production annuelle d’électricité (avec un vent de vitesses différentes).
Nombre équivalent d’heures à la puissance nominale = tN = EELEC/PN.
Valeur typique pour les grandes éoliennes en Wallonie : Tn = 25% de l’année.
Valeur typique pour les petites énergies éoliennes en Wallonie Tn = 11% de l’année.
Généralement, la production électrique annuelle d’une grande éolienne en Wallonie équivaut à 25% du temps à capacité nominale. Il ne faut pas conclure que l’éolienne n’est que de 25% du temps tourne. Non, dès que la vitesse actuelle du vent dépasse la vitesse du vent, l’éolienne conduit de l’électricité. En fait, les chiffres montrent que l’éolienne fonctionne 80 % du temps (source :
APERE). Malgré cela, il produit avec une puissance généralement inférieure à la puissance nominale, ce dernier souvent considéré comme la puissance maximale.
Estimation rapide : Analyse rapide
Dans certaines situations, en particulier dans le cadre d’une étude de préfaisabilité, nous aimerions être en mesure d’estimer approximativement ce qu’un site peut donner en tant que production. Vous pouvez simplement compter sur la vitesse moyenne du vent à, sur le site :
Estimation de la production = (rendement total moyen) * (1/2*Rho* A* (Um) 3)
Lorsque le rendement moyen est pris :
- 22% pour les petites éoliennes (moins de 35 m diamètre) ;
- 30% pour l’énergie éolienne moyenne (35 à 100 m de diamètre) ;
- et 35 % pour les grandes énergies éoliennes (> 100 m de diamètre).
En réalité, il y a une tendance à améliorer l’efficacité des modèles d’éoliennes avec les pales de rotor les plus longues (> 30 m) : Le graphique est basé sur 62 fiches techniques des éoliennes les plus récentes.
Nous savons très bien qu’il s’agit d’une estimation limitée, puisque l’effet des fluctuations de vitesse autour de la moyenne n’est pas pris en compte. On peut montrer que ce type d’estimation de l’énergie éolienne (le deuxième terme à droite) est susceptible d’entraîner de grandes erreurs. Le potentiel du vent est sous-estimé. Toutefois, si un constructeur prétend pouvoir produire une puissance électrique annuelle à une vitesse moyenne supérieure à quatre ou cinq fois celle de l’estimation simplifiée, vous pouvez clairement conclure qu’il ne s’agit pas d’une proposition honnête.
La limite de Betz
Le fabricant d’une éolienne doit certifier les caractéristiques de performance de son modèle. Cela doit se faire par une méthode normalisée, idéalement par l’intermédiaire d’un laboratoire indépendant.
Dans la pratique, les modèles moins performants ne bénéficient pas de cette certification. Le fabricant peut faire une courbe de performance, mais il n’y a aucune garantie de leur fiabilité, nous pouvons compter sur la crédibilité du fabricant au plus.
Comment reconnaissez-vous un produit fou ? Malheureusement, il n’y a pas de méthode absolue (sauf tester le matériel). Cependant, certains numéros fournis par le fabricant peuvent être testés. C’est le cas de l’efficacité globale instantanée de l’éolienne telle que définie dans la section précédente.
L’ application des principes de base de la mécanique permet d’utiliser pour déterminer la quantité maximale d’énergie éolienne qui peut être convertie en énergie mécanique (rotation du rotor). Le rendement aérodynamique instantané ou le coefficient de puissance (Cp) ne doit pas dépasser 16/27 ou environ 59 %. Par conséquent, l’efficacité instantanée, qui prend également en compte d’autres pertes (aérodynamique, accouplement, conversion électrique, puissance auxiliaire), doit être inférieure à cette valeur
: Efficacité globale immédiate < efficacité aérodynamique < 16/27
Cette limitation est mieux connue sous le nom de « betz limit » ou « théorie de betz ». Des hypothèses simplifiées ont dû être introduites pour parvenir à ces conclusions. Néanmoins, ces mesures sont tout à fait raisonnables.
Vitesse maximale et performance du garde-boue : rapport de vitesse de pointe
Il a été démontré que la limite de conversion de l’énergie éolienne en performance mécanique du rotor par l’approche Betz est théoriquement limité à 16/27 ou 59%. Par rapport à cet idéal, il existe un certain nombre d’imperfections qui empêchent l’atteinte de cette limite. En d’autres termes, nous avons un certain nombre de pertes qui réduisent l’efficacité aérodynamique de l’éolienne :
- Rotation de sillage : Le vent avant que le vent ne frappe l’éolienne n’a pas de mouvement de rotation prononcé et constant. De moins, c’est le cas si vous ne rencontrez pas d’obstacles majeurs devant l’éolienne. Une fois que l’air a passé le rotor de l’éolienne, il se produit à une vitesse générale de rotation dans la direction opposée du rotor. Cette vitesse de rotation inexistante correspond initialement à une certaine quantité d’énergie cinétique qui ne pouvait pas être convertie en éolienne. Il s’agit là d’une source principale de pertes.
- Piste des profils d’aile : Lorsque vous placez une aile face au vent, il crée de l’énergie sur cette aile. C’est l’effet attendu. Cette force peut s’effondrer partiellement. Force de flottabilité perpendiculaire à la direction du vent après l’aile, et un soi-disant composant de remorquage parallèle à cette vitesse du vent. Dans le cas d’un avion, l’ascenseur surmonte la gravité et permet à l’avion de voler comme ça. Trail freinage de l’avion parce que cette force est contraire à la direction dans laquelle le plan progresse. Pour que l’avion puisse maintenir cette vitesse, les moteurs de l’avion fournissent la puissance nécessaire pour vaincre cette résistance. Avec une éolienne, nous trouvons la même idée. Néanmoins, il est nécessaire de prendre en compte à la fois la vitesse du vent et la vitesse de rotation de l’éolienne. Le problème est un peu plus compliqué. Tout cela est pris en compte que la posture de la pâle de l’éolienne a une force utile dans le sens de rotation de l’éolienne. La résistance pâle, au contraire, ralentit la progression de ces pâleurs. Il s’agit d’une deuxième source de perte, car une partie de l’énergie éolienne est utilisée pour freiner l’éolienne. Heureusement, une aile d’éolienne est conçue pour fournir la plus faible résistance possible pour un levage particulier. Fondamentalement, il s’agit d’une question de spécialistes dans la mesure où il s’agit de travailler sur l’aérodynamique de l’aile.
- Nombre limité de pales de rotor : Le nombre de pales de rotor dans une éolienne est limité en termes de poids et de prix. Le rendement idéal considéré ci-dessus suppose un très grand nombre de lames. En réalité, ce chiffre ne sera jamais atteint. Cette restriction est à l’origine d’une troisième forme de perte. D’un point de vue physique, ces pertes sont générées par la résistance à l’air induite. La résistance à l’air induit est le plus bas, puisque la course est faible et le rapport de l’envergure à la corde moyenne de l’aile est important. Par conséquent, une ceinture qui a une grande travée par rapport à la corde aura une résistance plus faible. Cela peut être convaincu en comparant les ailes d’un planeur à celles d’un plan traditionnel : les pales du planeur sont beaucoup plus allongées pour limiter la résistance à l’air, ce qui est souhaitable puisqu’il n’a pas de moteur. C’est l’une des raisons pour lesquelles une éolienne a des ailes allongées.
**
L’ analogie entre l’allongement (rapport d’aspect) des ailes d’un planeur et les pales du rotor d’une éolienne : limitation de la résistance.
Ces explications visaient seulement à montrer que le rendement idéal n’a jamais été atteint, ce qui était dû à des pertes différentes. UN Le facteur qui influe fortement sur ces pertes est le rapport entre la vitesse d’extrémité de la feuille (induite par la rotation) et la vitesse du vent, le rapport basse-vitesse (TSR) en anglais,
Lambda = rapport bas-vitesse (TSR) = U/V = No.2*Pi*R/V,
avec,
- u, la vitesse maximale de la lame qui peut être considérée comme un produit
- la vitesse de rotation, n (en Hz),
- multiplié par le rayon de l’éolienne R par 2*pi.
- V est la vitesse du vent hors courant.
La théorie confirmée par la pratique montre que les pertes pour un RSV particulier sont minimisées. En d’autres termes, pour chaque vitesse du vent, il y a une vitesse de rotation qui maximise l’efficacité aérodynamique de l’éolienne, c’est-à-dire la quantité d’énergie éolienne transférée au rotor. Cela peut être fait en utilisant les peut être vu dans l’image
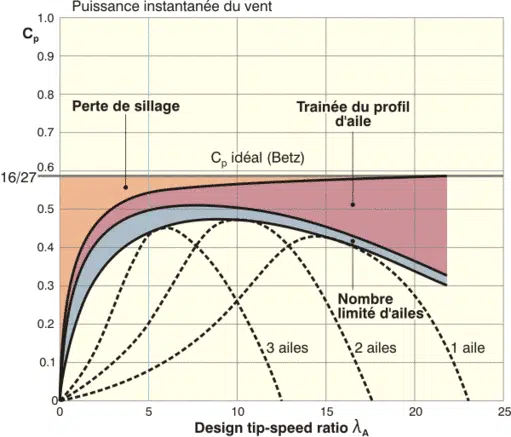
Développement de performances aérodynamiques instantanées dans le rapport vitesse d’extrémité de la feuille et vitesse d’inclinaison : illustration des différentes sources de perte par rapport au rendement idéal de Betz.
Le graphique peut être compris comme suit :
- Nous avons initialement la puissance éolienne immédiate par m², ce qui correspond au niveau de 100% dans le graphique.
- La théorie de Betz nous dit qu’au mieux nous pouvons récupérer jusqu’à 16/27 ou environ 60%.
- Si l’éolienne tourne plus lentement à une certaine vitesse du vent, nous avons un couple aérodynamique important pour obtenir la même puissance et, par conséquent, une forte déviation du fluide à travers les pales. Cela conduit à une rotation plus forte du parcours et, par conséquent, à de plus grandes pertes. Ceci est illustré dans le graphique sous le nom « Pertes de sillage ». En conclusion, plus l’éolienne tourne rapidement, moins les pertes de rotation sont faibles.
- En examinant le profil d’une pale d’éolienne, la force aérodynamique se décompose en une force de flottabilité, mais aussi en résistance à l’air qui résiste dans le sens de rotation de l’éolienne (du moins pour les éoliennes dont le principe de fonctionnement est basé sur la flottabilité). L’effet négatif sur l’efficacité aérodynamique est d’autant plus important que l’éolienne fonctionne rapidement. Cela peut être vu dans le diagramme ci-dessus sous le nom de « traînée du profil d’aile », où les pertes augmentent avec le rapport basse-vitesse. D’après les deux premières conditions de perte (perte de sillage et résistance au profil), une première optimale apparaît à une vitesse de pointe relative de l’aile entre 6 et 8.
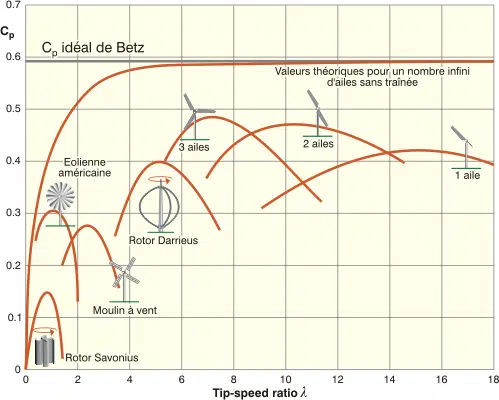
- Enfin, nous voyons la dernière période de perte causée par le nombre limité de lames volonté. Si nous prenons la courbe par rapport à un certain nombre de lames pointillées (nous regardons ici 1, 2 ou 3 ailes), nous voyons que la courbe générale est l’enveloppe de tous les maxima des courbes de nombre fixes.
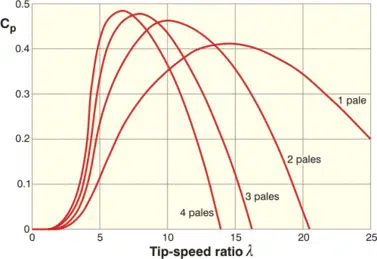
Changements dans les performances aérodynamiques en fonction du nombre de pales pour un modèle particulier.
En ce qui concerne la courbe ci-dessus, qui reflète l’évolution des performances aérodynamiques en fonction du nombre de pales pour un modèle particulier, nous voyons que plus le nombre de pales est élevé, plus le rapport de vitesse optimal à l’extrémité de la pale est faible.
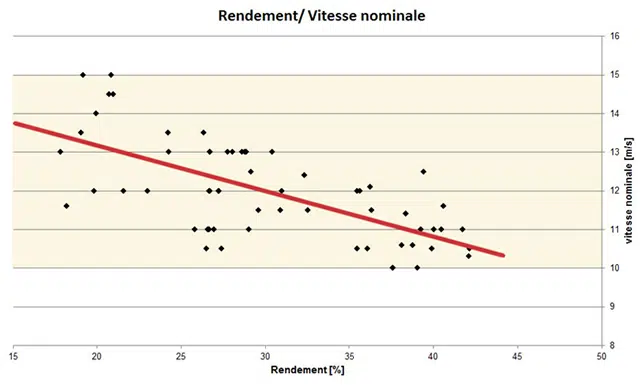
En outre, l’analyse du rendement de 62 modèles récents d’éoliennes montre qu’il existe une nette tendance à une meilleure efficacité pour les éoliennes ayant une vitesse nominale plus faible (de 10 m/s à 12 m/s).
Cette section peut être complétée en décrivant les différentes courbes de performance aérodynamique caractéristiques de chaque modèle d’éolienne majeure. En général, nous voyons que les éoliennes à flottabilité, c’est-à-dire les éoliennes Darrieus à axe horizontal ou vertical, ont un rendement aérodynamique plus élevé que les éoliennes basées sur le remorquage (habituellement le rotor Savonius). L’impact du nombre de lames sur les performances est également montré. À mesure que la vitesse de rotation diminue, un couple aérodynamique plus important est nécessaire pour la même puissance mécanique. Pour cette raison, les éoliennes souhaitant effectuer des travaux mécaniques, en particulier pour des applications de pompes, ont un nombre important de pales de rotor (illustré par l’éolienne américaine ci-dessous). À l’heure actuelle, les éoliennes Darrieus ont un Efficacité comme indiqué dans le tableau ci-dessous.
Développement typique du rendement aérodynamique selon le rapport de vitesse de kip-vitesse et le modèle d’éolienne.